Walking around of New York City, you’re free to choose your own path. Because of the ubiquitous grid-like layout of most of the city, the path that you take between any two points has the same distance no matter what individual turns you make. Known as taxicab geometry, the normal Euclidian distance formula that we’re familiar with is replaced with a formula that depends only on the north-south and east-west distances. The distance itself is slightly longer (by 41%, in the worst case), since you can’t cut through blocks and go “as the crow flies” , but no matter the path, the distance is always the same.
Combinatorics provides us with the precise number of combinations between two points. Let’s say I have a 40x20 grid of city blocks that I need to get through. Walking between them, I’ll have to go to the right 40 times, and to the left 20 times, for a total of 60 segments. The order that I make these steps doesn’t matter, and so there are C(60, 20) = 4,191,844,505,805,495 unique routes between these two points in the grid. For those that follow Project Euler, this is problem 15.
If you consider that for each block segment, there are two possible sides to the street, then you get an even larger number of possibilities, since each segment adds a factor of two to the possible paths. So for the 40x20 case above, the total number of paths would be..
C(60, 20) \* 2 60
..which is approximately 4.83 x 10 33 unique routes. Even taking the same few blocks to and from work every day, you end up seeing a lot of interesting variety. Whether different styles of architecture, plants, parks, or small pieces of human creativity, the city has a lot to offer for pedestrians. It’s tempting to just scurry along the same beaten path every day, but for those who seek novelty there is a lot to find when meandering the veins and arteries of the city.

New York isn’t the first nor only city with grids — but due to its unique geology it’s more accessible than other cities. For example, even though large parts of San Francisco are organized in orderly grids, the huge altitude changes between hills and valleys preclude random walks as an efficient means of transportation.
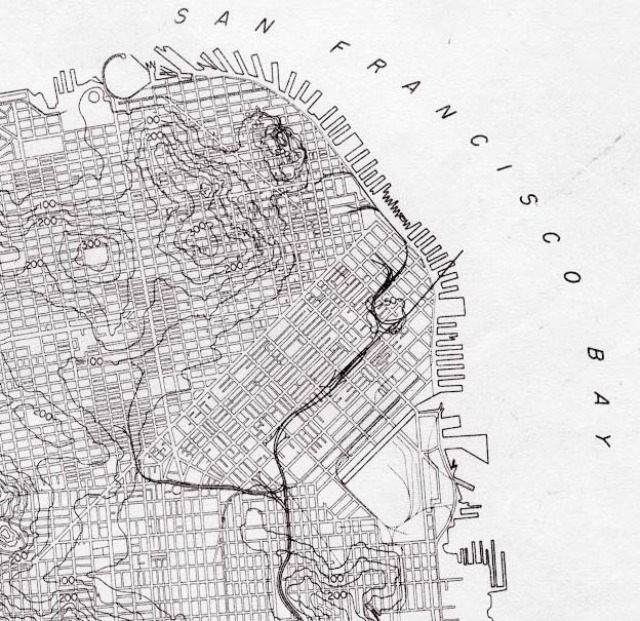
Popular bike and walking routes like The Wiggle are a result of this topology. Even though there are over 1,200 possible routes connecting the two end points of the Wiggle, which are separated by only one mile, bikers and pedestrians swear by the low-incline path.
Other cities, like Brazil’s Belo Horizonte, have their own twist on the traditional city grid, overlaying two offset grids on top of one another:
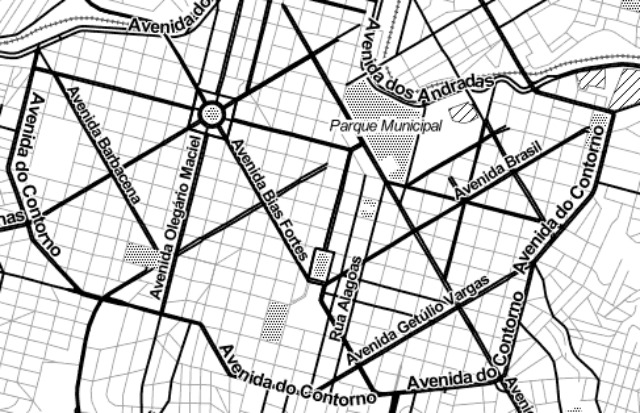
While the orderliness of grids stands in opposition to the whims of nature and geological history, they not only contribute to the organization of the modern city but also greatly affect those living within it.